平面直角坐标系中直角三角形存在性问题

在本文中，我们将从矩形和正方形的判定入手，选择合适的方法解决平面直角坐标系中矩形和正方形的存在性问题。

一、判定方法

矩形的判定定理有3条：①对角线相等的平行四边形是矩形；②有一个角是直角的平行四边形是矩形；③3个角是直角的四边形是矩形。

判定③对应在坐标系中就是使用勾股定理，这样的计算过程比较复杂，因此判定③不做为选择的方法。

矩形的存在性问题的题型往往是“两定点+一个半动点+一个全动点”，以边和对角线进行分类讨论。当两定点所在线段为矩形的对角线时，往往利用判定①画出图形，利用矩形对角线得对角线互相平分且相等来做；当两定点所在线段为矩形的一边时，往往利用判定②画出图形，利用勾股定理或锐角三角比解决问题。我们的解题思路是“先Rt再平四”，即选择半动点构造直角三角形，利用平行四边形的对称性求出全动点坐标。

二、具体分析

分析：(1)直线l的解析式为:y=2x+2，B(0,2)，C(1,4).

(2)矩形的两定点为A、C，以AC为边或对角线进行分类讨论，构造Rt▲PAC，先求出点P的坐标，再利用平行四边形对称性求出点Q坐标。值得注意的是，本题中的矩形限定了情况，因此通过画图，排除不符合题意得情况。

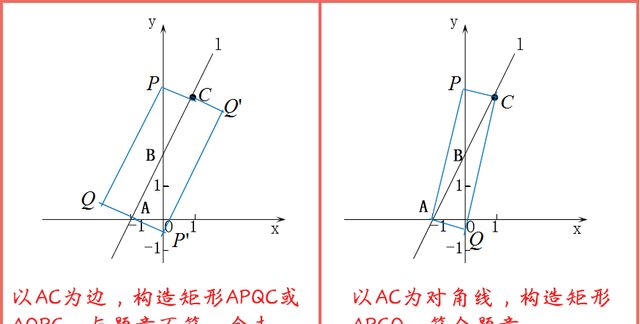
思考：若以A、P、C、Q四个点为顶点的四边形是矩形，如何求P、Q坐标？

再补充上AC为边的情况即可。

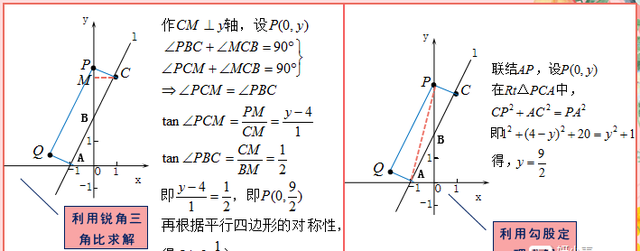
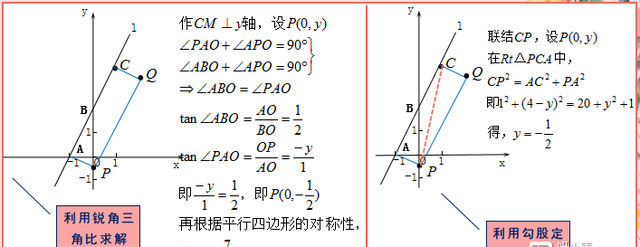
其实矩形的存在性问题就是直角三角形的存在性问题，先通过对称或勾股定理或相似三角形确定半动点的坐标，再根据平行四边形的对称性求出第四点的坐标。

一、判定方法

正方形由于其特殊性(四个角是直角及四边相等)，往往通过构造一线三等角模型，利用三角形全等求出点坐标。常见的题型也是“两个顶点+一个半动点+一个全动点”。

二、构造模型

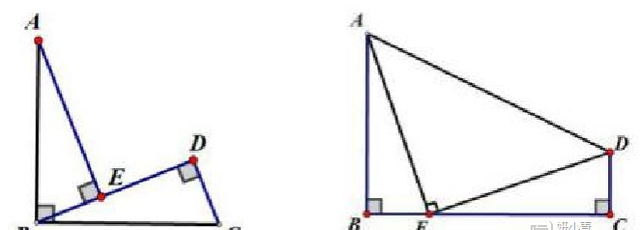
如左图，▲ABC为等腰直角三角形，利用平行四边形的对称性，可以求出第四点坐标；如右图，▲AED为等腰直角三角形，利用平行四边形的对称性，可以求出第四点坐标。因此，正方形的存在性问题就是利用构造的全等三角形求出点的坐标。

三、具体分析

题型1：已知正方形，求相应点的坐标

题型2：已知两定点+一半动点+一全动点，解决正方形的存在性问题。

分析：(1)本题的关键要发现BE⊥BC；(2)以▲OCB为目标三角形构造一线三等角模型，本题只要求E点坐标，F点坐标可以通过平行四边形的对称性求得。

分析：(1)角平分线和平行线必出现等腰三角形。证明EB=OB,BF=OB，即可得证。(2)对角线互相平分且相等的四边形是矩形。因为(1)已经证明了EB=BF=OB，只要满足OB=BA，即可证明EOFA为矩形，因此OB:OA=1:2；(3)由于AEOF为正方形，因此OA与EF垂直。对角线EF，已经与x轴平行，因此另一条对角线OA必然与x轴垂直。即A在y轴上，因此A(0,4)，B(0,2)。

其实矩形的存在性问题就是等腰直角三角形的存在性问题，先通过一线三等角模型确定半动点的坐标，再根据平行四边形的对称性求出第四点的坐标。